若您覺得文章寫得不錯，請點選文章上的廣告，來支持小編，謝謝。
作品連結：https://scratch.mit.edu/projects/119509570/
Demo影片：
HTML5 Canvas 基礎 ( HTML5 Canvas Basic )
若您覺得文章寫得不錯，請點選文章上的廣告，來支持小編，謝謝。
If you like this post, please click the ads on the blog. Thank you very much.
If you like this post, please click the ads on the blog. Thank you very much.
Canvas是一個可以在上面畫東西的畫紙例如可以畫圓、畫矩形等，而Canvas的座標系統的原點在最左上角，Y軸向下遞增，X軸向右遞增(見下圖)。
The HTML Canvas is a element used to draw some graphics(circles, rectangles, lines, etc.) on it. And the Canvas coordinates system is on the figure:
那我們就來畫個小精靈吧！
Let's draw a Pac-Man.
The HTML Canvas is a element used to draw some graphics(circles, rectangles, lines, etc.) on it. And the Canvas coordinates system is on the figure:
那我們就來畫個小精靈吧！
Let's draw a Pac-Man.
簡單介紹JSON是什麼玩意兒？ ( Short introduction to JSON )
若您覺得文章寫得不錯，請點選文章上的廣告，來支持小編，謝謝。
JSON的全名為JavaScript Object Notation，提供便利又易懂方法來儲存資訊，下面就是一個簡單的例子：
JSON的語法是以"name": "value"來運作，上述例子建立了一個holan的變數，儲存了age、hometown、gender三項資訊。
下面是陣列的例子：
有時會需要驗證JSON的語法，此網頁：http://jsonlint.com/可幫助我們做到這件事。
JSON的全名為JavaScript Object Notation，提供便利又易懂方法來儲存資訊，下面就是一個簡單的例子：
JSON的語法是以"name": "value"來運作，上述例子建立了一個holan的變數，儲存了age、hometown、gender三項資訊。
下面是陣列的例子：
有時會需要驗證JSON的語法，此網頁：http://jsonlint.com/可幫助我們做到這件事。
C語言的指標與陣列 ( Pointer and array in C )
若您覺得文章寫得不錯，請點選文章上的廣告，來支持小編，謝謝。
陣列與指標 from PingLun Liao
底下列出幾篇不錯的文章供參考：
[1] 指標與記憶體位址：http://openhome.cc/
Arduino Esplora碼錶 ( Arduino Esplora Stopwatch )
若您覺得文章寫得不錯，請點選文章上的廣告，來支持小編，謝謝。
功能上跟簡易 Java 碼錶差不多，也就不解釋太多。因為Java是用JLabel中的Text Property，所以沒有需要程式處理重繪的問題，但是Arduino Esplora就得處理了。
程式語言中，變數名稱的長度會不會影響程式的效能或大小？
若您覺得文章寫得不錯，請點選文章上的廣告，來支持小編，謝謝。
我把此問題拿去問Jserv，想不到他回了我這個小人物的EMail！
所以就簡短複習一下Compiler Design的內容，編譯器要做的事就是將程式碼翻譯成機器看得懂的語言(目標語言)，有些原因讓編譯器不直接這樣子處理，而是先轉成中間碼再轉為目標語言。
Source code ==> Intermediate Code ==> Assembly Code
而在中間碼轉為目標語言會做優化的動作，不同的編譯器所實作的優化方法不一樣，而且就算是相同的編譯器也有不同的優化層級(如GCC)。這也是為什麼編譯器會持續不斷更新的原因之一。
換個方式說明好了，以中文作文翻譯成英文作文時，不同的人翻譯出來的英文作文字數(大小)會不一樣，就算是相同的人，翻譯的字選也有多個選擇。而優秀的翻譯人員所翻譯出來的英文作文通順流暢(效能)，而像我這種外行人(品質差的編譯器)翻譯出來的英文作文超不通順的。
男兒們阿，別再在乎長度了好不好！
我把此問題拿去問Jserv，想不到他回了我這個小人物的EMail！
所以就簡短複習一下Compiler Design的內容，編譯器要做的事就是將程式碼翻譯成機器看得懂的語言(目標語言)，有些原因讓編譯器不直接這樣子處理，而是先轉成中間碼再轉為目標語言。
Source code ==> Intermediate Code ==> Assembly Code
而在中間碼轉為目標語言會做優化的動作，不同的編譯器所實作的優化方法不一樣，而且就算是相同的編譯器也有不同的優化層級(如GCC)。這也是為什麼編譯器會持續不斷更新的原因之一。
換個方式說明好了，以中文作文翻譯成英文作文時，不同的人翻譯出來的英文作文字數(大小)會不一樣，就算是相同的人，翻譯的字選也有多個選擇。而優秀的翻譯人員所翻譯出來的英文作文通順流暢(效能)，而像我這種外行人(品質差的編譯器)翻譯出來的英文作文超不通順的。
男兒們阿，別再在乎長度了好不好！
整數四則運算練習題
若您覺得文章寫得不錯，請點選文章上的廣告，來支持小編，謝謝。
練習一：
求下列各式的值：
(1) \(3 - 6\)
(2) \(10.234 - 11\)
(3) \(1\dfrac{3}{5} - 10.8 \)
答案：
(1) \(3 - 6 = -(6 - 3) = -3 \)
(2) \(10.234 - 11 = -(11 - 10.234) = -0.766 \)
(3) \(1\dfrac{3}{5} - 10.8 = 1.6 - 10.8 = -(10.8 - 1.6) = -9.2\)
練習二：
求下列各式的值：
(1) \(|3 - 6|\)
(2) \(|10.234 - 11|\)
(3) \(|1\dfrac{3}{5} - 10.8|\)
答案：將練習一的負號去掉即為答案。
練習三：
(1) \(-3 - 6\)
(2) \(-3 - 6 - (-7) \)
(3) \(-3 + (-6) - (-7) \)
答案：
(1) \(-3 - 6 = (-3) + (-6) = -(3+6) = -9\)
(2) \(-3 - 6 - (-7) = (-3) + (-6) + 7 = -(3+6) + 7 = -9 + 7 = -(9-7) = -2\)
(3) \(-3 - (-6) - (-7) = (-3) + 6 + 7 = 13 - 3 = 10\)
練習四：
(1) \(-4 \times 25\)
(2) \( -3 \times -3\)
(3) \( (-3)^5 \)
(4) \( (-100) \div 5 \times (-2)\)
(5) \( (10-12) \times (-3) \div 3 \)
答案：
(1) \(-4 \times 25 = -(4\times 25) = -(100) = -100\)
(2) \( -3 \times -3 = 3 \times 3 = 9 \)
(3) \( (-3)^5 = (-3) \times (-3) \times (-3) \times (-3) \times (-3) = -243\)
(4) \( (-100) \div 5 \times (-2)\ = 100 \div 5 \times 2 = 20 \times 2 = 40\)
(5) \( (10-12) \times (-3) \div 3 = -(12 - 10) \times (-3) \div 3 = (-2) \times (-3) \div 3 = 2 \times 3 \div 3 = 6 \div 3 = 2\)
練習一：
求下列各式的值：
(1) \(3 - 6\)
(2) \(10.234 - 11\)
(3) \(1\dfrac{3}{5} - 10.8 \)
答案：
(1) \(3 - 6 = -(6 - 3) = -3 \)
(2) \(10.234 - 11 = -(11 - 10.234) = -0.766 \)
(3) \(1\dfrac{3}{5} - 10.8 = 1.6 - 10.8 = -(10.8 - 1.6) = -9.2\)
練習二：
求下列各式的值：
(1) \(|3 - 6|\)
(2) \(|10.234 - 11|\)
(3) \(|1\dfrac{3}{5} - 10.8|\)
答案：將練習一的負號去掉即為答案。
練習三：
(1) \(-3 - 6\)
(2) \(-3 - 6 - (-7) \)
(3) \(-3 + (-6) - (-7) \)
答案：
(1) \(-3 - 6 = (-3) + (-6) = -(3+6) = -9\)
(2) \(-3 - 6 - (-7) = (-3) + (-6) + 7 = -(3+6) + 7 = -9 + 7 = -(9-7) = -2\)
(3) \(-3 - (-6) - (-7) = (-3) + 6 + 7 = 13 - 3 = 10\)
練習四：
(1) \(-4 \times 25\)
(2) \( -3 \times -3\)
(3) \( (-3)^5 \)
(4) \( (-100) \div 5 \times (-2)\)
(5) \( (10-12) \times (-3) \div 3 \)
答案：
(1) \(-4 \times 25 = -(4\times 25) = -(100) = -100\)
(2) \( -3 \times -3 = 3 \times 3 = 9 \)
(3) \( (-3)^5 = (-3) \times (-3) \times (-3) \times (-3) \times (-3) = -243\)
(4) \( (-100) \div 5 \times (-2)\ = 100 \div 5 \times 2 = 20 \times 2 = 40\)
(5) \( (10-12) \times (-3) \div 3 = -(12 - 10) \times (-3) \div 3 = (-2) \times (-3) \div 3 = 2 \times 3 \div 3 = 6 \div 3 = 2\)
燒錄 Bootloader 至 Arduino Uno R3 上的 atmega328 ( How to upload a bootloader to Arduino UNO atmega328 )
若您覺得文章寫得不錯，請點選文章上的廣告，來支持小編，謝謝。
If you like this post, please click the ads on the blog. Thank you very much.
If you like this post, please click the ads on the blog. Thank you very much.
某位同事問我：「你有用Arduino Uno當 ISP 燒錄器來燒錄bootloader嗎？」
「沒實際用過，但看過教學文章。」底下就是我參考的文章：
將Arduino Uno當做一台ISP線上燒錄器，燒錄bootloader或sketch到麵包板上的ATmega328P-PU晶片
「沒實際用過，但看過教學文章。」底下就是我參考的文章：
將Arduino Uno當做一台ISP線上燒錄器，燒錄bootloader或sketch到麵包板上的ATmega328P-PU晶片
簡單整理一下軟體燒錄的流程：
To sum up the bootloader uploading steps:
To sum up the bootloader uploading steps:
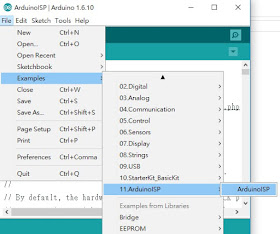
1. 燒錄ArduinoISP範例在一塊Uno板子上，讓它當成ISP燒錄器(底下稱為Uno ISP板)。
1. Upload ArduinoISP example code in a Arduino UNO for being an AVR ISP.
2. 將線路接好，Uno ISP板連接主機電腦後，開啟Arduino IDE 軟體。
2. After connecting the circuit, the AVR ISP is ready. Then, open Arduino IDE.
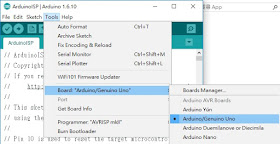
3. 設定 Tools ==> Board 選為 Uno。
3. Configure the board as "Arduino/Genuino Uno"
4. 設定 Tools ==> Serial Port。
4. Select your AVR ISP serial port number.
5. 設定 Tools ==> Programmer為Arduino as ISP。
5. Configure programmer as "AVR ISP"
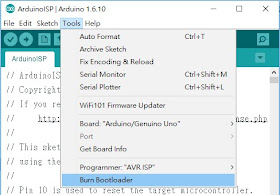
6.執行 Tools ==> Burn Bootloader。
6. Execute "Burn Bootloader"
6. Execute "Burn Bootloader"
便可將 bootloader 燒錄到 ATmega328P-PU晶片，此外若沒燒錄 bootloader 的話，將無法用Uno板去燒錄韌體到ATmega328P-PU晶片裡。
Right now, we have burnt bootloader into ATmega328P-PU. The Arduino IDE can't upload any code to UNO without the bootloader.
Right now, we have burnt bootloader into ATmega328P-PU. The Arduino IDE can't upload any code to UNO without the bootloader.
部份分式 Partial Fractions
若您覺得文章寫得不錯，請點選文章上的廣告，來支持小編，謝謝。
問題一
\[\dfrac{2x+1}{(x+1)(x-3)(x+4)} = \dfrac{A}{(x+1)}\ + \dfrac{B}{(x-3)}\ + \dfrac{C}{(x+4)}\]
上列式子中，\(A + B + C\)為多少？問題一
\[\dfrac{2x+1}{(x+1)(x-3)(x+4)} = \dfrac{A}{(x+1)}\ + \dfrac{B}{(x-3)}\ + \dfrac{C}{(x+4)}\]
解法一：
左右兩邊同乘\((x+1)(x-3)(x+4)\)得到\[2x+1 = A(x+4)(x-3)+B(x+4)(x-1)+C(x+1)(x-3)\]
\(x = -4\) 代入得 \(-7 = C \times -3 \times -7 \) ==> \(C = \dfrac{-1}{3}\)
\(x = -3\) 代入得 \(7 = B \times 7 \times 4 \) ==> \(B = \dfrac{1}{4}\)
\(x = -1\) 代入得 \(-1 = A \times 3 \times -4 \) ==> \(A = \dfrac{1}{12}\)
所以 \( A + B + C = \dfrac{1}{12} + \dfrac{1}{4} + \dfrac{-1}{3} = \boxed{0}\)
解法二：
原式改寫為 \(\dfrac{2x+1}{(x+1)(x-3)(x+4)} \\ = \dfrac{A}{x+1} + \dfrac{B}{x-3} + \dfrac{C}{x+4}\\ =\dfrac{A(x-3)(x+4) + B (x+1)(x+4) + C(x+1)(x-3)}{(x+1)(x-3)(x+4)}\)因為分母相同，所以比較分子的係數：
\(A(x^2 +x -12) + B (x^2+5x+4) + C(x^2-2x-3) = 2x+1\\ (A+B+C)x^2 + (A+5B-2C)x +(-12A+4B-3C) = 2x+1\)
可得到
\((A+B+C)x^2 = 0x^2\\ A+B+C = \boxed{0}\)
問題二
\[\dfrac{x^2 - 19}{x^3 - 2x^2 -5x + 6} = \dfrac{A}{x-1} + \dfrac{B}{x+2} + \dfrac{C}{x-3}\]
上式中\(A,B, C\) 為常數，求\(A\times B\times C\)為多少？\((A+B+C)x^2 = 0x^2\\ A+B+C = \boxed{0}\)
問題二
\[\dfrac{x^2 - 19}{x^3 - 2x^2 -5x + 6} = \dfrac{A}{x-1} + \dfrac{B}{x+2} + \dfrac{C}{x-3}\]
解法一：
\[\dfrac{x^2 - 19}{x^3 - 2x^2 -5x + 6} = \dfrac{A}{x-1} + \dfrac{B}{x+2} + \dfrac{C}{x-3}\]
\[\Rightarrow x^2 - 19 = A(x+2)(x-3) + B(x-1)(x-3) + C(x-1)(x+2)\]
\[\begin{cases} x=1\quad \quad \Rightarrow \quad 18=-6A\quad \, \, \, \Rightarrow \quad A=3 \\ x=-2\quad \, \Rightarrow \quad -15=15B\quad \Rightarrow \quad B=-1 \\ x=3\quad \quad \Rightarrow \quad -10=10C \quad \Rightarrow \quad C=-1 \end{cases}\]
\[ \Rightarrow ABC = -1 \times 3 \times -1 = \large \color{green}{\boxed{3}}\]
解法二：
\[\dfrac{x^2 - 19}{x^3 - 2x^2 -5x + 6} = \dfrac{A}{x-1} + \dfrac{B}{x+2} + \dfrac{C}{x-3}\]
\[\dfrac{x^2 - 19}{(x-1)(x+2)(x-3)} = \dfrac{A(x+2)(x-3) + B(x-1)(x-3) + C(x-1)(x+2)}{(x-1)(x+2)(x-3)}\]
\[\dfrac{x^2 - 19}{(x-1)(x+2)(x-3)} = \dfrac{A(x^2 - x -6) + B(x^2 - 4x + 3) + C(x^2 + x - 2)}{(x-1)(x+2)(x-3)}\]
\[\dfrac{x^2 - 19}{(x-1)(x+2)(x-3)} = \dfrac{(A+B+C)x^2 + (C-A-4B)x + (3B-6A-2C)}{(x-1)(x+2)(x-3)}\]
觀察兩邊的係數，可得：
\[\begin{cases}A+B+C=1\\C-A-4B=0\\3B-6A-2C= -19\end{cases}\]
\[\Rightarrow x^2 - 19 = A(x+2)(x-3) + B(x-1)(x-3) + C(x-1)(x+2)\]
\[\begin{cases} x=1\quad \quad \Rightarrow \quad 18=-6A\quad \, \, \, \Rightarrow \quad A=3 \\ x=-2\quad \, \Rightarrow \quad -15=15B\quad \Rightarrow \quad B=-1 \\ x=3\quad \quad \Rightarrow \quad -10=10C \quad \Rightarrow \quad C=-1 \end{cases}\]
\[ \Rightarrow ABC = -1 \times 3 \times -1 = \large \color{green}{\boxed{3}}\]
解法二：
\[\dfrac{x^2 - 19}{(x-1)(x+2)(x-3)} = \dfrac{A(x+2)(x-3) + B(x-1)(x-3) + C(x-1)(x+2)}{(x-1)(x+2)(x-3)}\]
\[\dfrac{x^2 - 19}{(x-1)(x+2)(x-3)} = \dfrac{A(x^2 - x -6) + B(x^2 - 4x + 3) + C(x^2 + x - 2)}{(x-1)(x+2)(x-3)}\]
\[\dfrac{x^2 - 19}{(x-1)(x+2)(x-3)} = \dfrac{(A+B+C)x^2 + (C-A-4B)x + (3B-6A-2C)}{(x-1)(x+2)(x-3)}\]
觀察兩邊的係數，可得：
\[\begin{cases}A+B+C=1\\C-A-4B=0\\3B-6A-2C= -19\end{cases}\]
解聯立方程式可得: \(A =3, B = -1, C = -1\)，因此\(A\times B\times C = 3\times -1\times -1 = \boxed{3}\).